←　その１(/２）へ

問　時系列の“ゆらぎ”の構造は，MemCalcではどのように調べるのですか？“基底変動”の場合とは異なるのですか？

0930

答　“基底変動”と“ゆらぎ”の構造を決めるためには，それぞれにふさわしいデータ長があります．大きなデータ長のデータを一括して小さい時間スケールで解析すると，小さな時間スケールの周期的変動の“ゆらぎ”の平均的構造しか明らかにできません．従来の時系列解析の多くはこうしたものでした．
　時々刻々変動する“ゆらぎ”を明らかにするためには，大きな時間スケールにわたる小さな時間スケールでの解析が必要です．問題は時間スケールをどこまで小さくすれば良いかという点にあります．一つの目安は，“ゆらぎ”の時間スケール程度にとることです．しかし，時系列データは，データの１点ごとに“ゆらぐ”場合もあり，この場合の時間スケールはデータの１点に相当する大きさになります．こうして，“ゆらぎ”は，時系列の“瞬間”の変動を問題にすることになります．即ち，最も精緻な“ゆらぎ”の解明は，時系列の“瞬間”の構造を明らかにすることと同義です．これは，スペクトル解析においては“瞬間スペクトル”を求めることを意味します．MemCalcでは，時系列の変動を生み出すシステムの“瞬間”の構造を問題にする立場から，時系列のセグメント解析を可能にしています． 

問　MemCalcでは，フラクタル構造を持つ時系列をどのように解析しているのですか？

0940

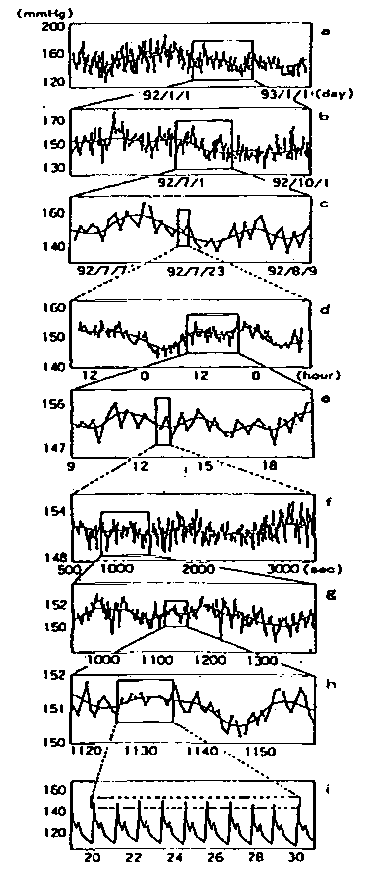
答　図0940は血圧の時系列データを示します．図0940の最上段(a図)の時系列では，年単位の時間スケールの“基底変動”が求められ，その時系列の任意の時間領域(四角囲み部分)を切り出して解析し，月単位の時間スケールの“基底変動”が求められます(b図)．同様に，b図の任意時間領域(四角囲み部分)を切り出して解析し，日単位の時間スケールの“基底変動”が求まります(c図)．MemCalcでは，こうした処理が極めて容易に実行できるようになっています．
　このように，MemCalcでは，大きな時間スケールで解析を行う場合，大きな時間スケールの変動を“基底変動”とみなし，小さな時間スケールの変動をその“基底変動”に対する“ゆらぎ”とみなして解析を進めます． 時系列をこうとらえ直すことによって，MemCalcでは，こうしたフラクタル構造をもつ時系列の解析を可能にしています．

図0940　血圧の時系列データのフラクタル構造．

問　MemCalcでは，時系列データのあてはめ曲線をどのように計算しているのですか？

0950

答　MemCalcでは，実用的な時間内で良好な結果を得るために，原時系列データに含まれる振動ないし波動の周期値のみをMEMスペクトルから別に求め，これにより問題を線形最小２乗法の問題として解いています．即ち，原時系列データ中のドミナントな一つまたは複数の振動の周期はMEMスペクトル中の一つまたは複数の鋭いピークのピーク周波数の逆数として求められます．この手続きは非線形最小２乗法に対して，新たな解法を与えるものです．

問　MemCalcでは，時系列データのあてはめ曲線の妥当性はどのようにして認められるのでしょうか？

0960

答　私たちは，時系列に対するあてはめ曲線の妥当性を測るために，原時系列からあてはめ曲線を差し引くことによって得られる残差時系列の標準偏差を調べます．図0920-1は，太陽黒点数時系列データをMemCalcでスペクトル解析し，MEM-PSDで評価される主要な周期モードを順次あてはめ曲線に取り込んだときに得られる標準偏差の変化を示しています．同図に見られるように，標準偏差はモード数の増加とともに減少します．この結果は，MemCalcで評価された周期の妥当性を示すものです．
　図0920-2は，最初の５モードを用いて計算されたあてはめ曲線の原データと比較を示しています(実線：あてはめ曲線，点線：原時系列データ)．同図に見られるように，あてはめ曲線(実線)は，原時系列データ(点線)の基底変動を十分に良く再現しています．このことは，図0920-1で６〜８モードの付近でSDの減少の度合が１〜５モードの場合よりも小さくなっていることからもわかります．こうして12個の周期の寄与は，２つの部分，即ち基底変動とゆらぎの部分に分けることができます．

問　MEMでスペクトルを求めると｢FFTでも計算したのか，その結果と比較検討したか．｣と尋ねられました．これは必要なことでしょうか？

0970

答　MEM，FFTなどの長所・短所・具体的使用の際のノウハウなどは，専門家によって数十年以上にわたって相当に詳細に検討されてきています．それらの展開を踏まえ，ともに同程度の今日的水準で同じデータについてMEMとFFTによるスペクトルを求めることは，困難なことです．ましてやそのことを通して与えられたデータに対するそれぞれの解析方法そのものの可否まで判断するなどということは，スペクトル解析法そのものについての研究者であるならば別かもしれませんが，事実上不可能です．
　スペクトル解析の専門書などに例示されているMEMなりFFTなりのサンプルプログラムをそのまま動かしても，けっして今日的水準でのそれぞれのスペクトルを得たことにはなりません．例えばMEM(Burg法)については，例示されたサンプルプログラムは高々数十行程度のものですが，MemCalcシステムでは対応する計算の核心部分が数千行にもなります．従ってサンプルプログラムによって得た結果をもってMEMとFFTの比較検討ができるなどと考えること自体，大変に馬鹿げた発想です． FFTの結果でデータとスペクトルが公開されているものについては，私たちはこの比較を行いました．詳しくは問1000を参照してください．

問　スペクトル解析というものを研究の道具として用いる立場から，具体的データについて，今日望み得る最も精確に計算されたMEMとFFTの結果を比較検討したいのですが，どのような方法が考えられますか？

0980

答　解析対象とするデータについて詳細な知識をもつ専門家がMEMの特徴を正しくとらえた上で，細心の注意を払ってMEMという道具立てを正しく用いて対象データのスペクトルを算出し，その結果を(対象に関する)専門家の立場から検討すること，そして，例えば研究の道具立てとしてFFTを用いる研究者の報告と照らし合わせることが考えられます．このとき，同種のデータならば，例えばスペクトルの傾きについては解析法によらず一定の範囲に収まらなければなりません．また，そのトータルパワーもデータにもよりますが，ある範囲に収まることが期待されます．このような点については，容易に検討できます．
　しかし，それ以上については，それぞれのスペクトル解析法の特徴を踏まえて正しく適用したかという点を検討した上で，最終的には対象に関する専門家として，それぞれの結果の示すところを判断する以外にありません．あるいはベンチマーク(bench mark)テストを行うことが必要です．これは，同一のデータについて，解析の専門家がそれぞれの解析法を駆使して，自らの方法でどういうことが引き出せるかを行い，それを公開することです．

問　報告されたスペクトルの“正当性”そのものについて検討する場合，どのような点に注意すべきですか？

0990

答　MEMにせよFFTにせよ，有限長の時系列データからそのスペクトルを“推定”するための道具にすぎません．このことは，逆にそれらを道具としてその特徴・限界をわきまえて正しく用いる必要のあることを意味します．
　例えばFFTは低周波数領域において計算点を周密に設定することができず，与えられた時系列データが無限に繰り返されることを前提とした理論体系と相俟って，低周波数帯でのスペクトルには相当の“誤差”が含まれます．低周波数帯を問題とする場合，データ長を長く取れるならば別ですが，そうでなければFFTの結果はMEMの結果に比較して精度の落ちることが予想されます．

問　スペクトルピークの周期値で元の時系列を再現することは可能ですか？

1000

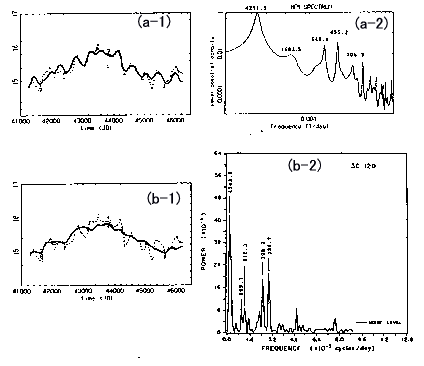
答　ここで，銀河3C 120の光度の変動(図1000(a-1)と(b-1)の点線)を例にして説明します．ウエッブら(Webb et al)はこのデータをFFTで解析し，図1000(b-2)に示されるFFT-PSDを得ました．FFT-PSDピークから決められた周期の値を用いて計算された最適LSF曲線が図1000(b-1)(実線)に示されています．FFT評価周期に基づくLSF曲線は原データを再現しません．一方，MEM-PSDが図1000(a-2)に示されています．MEM評価周期を用いて得られたLSF曲線は，原時系列データを基本的に再現しています(図1000(a-1))．従来スペクトル解析で得られた周期値の妥当性を検証する手段が無かったのですが，MemCalcを用いるとこれが可能であり，元の時系列さえ与えられれば，これまで報告されたスペクトルの妥当性をことごとく検証することが可能です．

図1000 FFT-PSDのピークとMEM-PSDのピークとの比較(銀河3C　120の光度の変動)．　

問　ホワイトノイズのスペクトルは定義上，周波数に依存しない一定値となるはずです．MemCalcでホワイトノイズのスペクトルを計算するとラグの小さいうちはほぼ一定値のスペクトルを示しますが，ラグを大きくとるとさまざまなピークが現れます．ピークの存在を別にすればこのスペクトルの傾きは０(フラット)となるようですが，なぜピークが現れるのですか？

1010

答　定義上，無限の長さをもつホワイトノイズのスペクトルは一定値を取ります．しかし，現実の時系列データは必ず有限長です．その結果，有限時系列データがどれほどホワイトノイズライクであったとしても，定義通りのホワイトノイズにはなり得ず，そのスペクトルにはピークが現れることになります．ピークが見いだされることは，有限長のデータの挙動は有限個の余弦函数の重畳として完全に記述できることに対応します．

問　MemCalcシステムではスペクトルの傾きをどのように求めているのでしょうか？特にスペクトルが鋭いピークをもつ場合，困難は生じませんか？

1020

答　ある周波数帯におけるスペクトルの傾きとは，周波数の変化に伴ってその周波数近傍のパワーがどのように変化するか，指定周波数帯全体にわたるその変化の傾向であるとすることができます．従ってMemCalcシステムではMEMスペクトルからある周波数の近傍の(平均)パワーを計算し，これらの値(周波数,パワー)の系列について最小二乗法により傾きを求めています．MemCalcシステムではスペクトルが鋭いピークをもつ場合でもその面積が正確に計算されますから，以上の手続きにより鋭いピークの存在が算出するスペクトルの傾きに悪影響を及ぼすことはありません．

問　スペクトルの傾きの妥当性はどのようにして客観的に測りますか？

1030

答　スペクトルの傾きとは，スペクトルのパワー値の傾向的減衰を示すものです．これは，スペクトル解析の分解能に依存するものではありません．従って，MemCalcにおいてラグ値を変化させ，極端な例では，ラグ１の最も粗い分解能で計算しても，傾きは元のまま不変になっていることが必要です(問1040参照)．
　しかし，これはある傾きをもつ時系列について成立することであり，その時系列がそもそもそういう傾きをもっているかどうかの検証が必要です．この検証は，理論的に厳密に求められるスペクトルの傾きをMemCalcが再現することができるかどうかを見ることによって達成されます．MemCalcはこの試練にも耐え，見事に理論計算を再現します(問1290参照)．これは大変重要で，且つ画期的な成果で，これまでのあらゆるスペクトル解析法でこれを実現することはできていません．

問　スペクトルの傾きは，ラグ値によって変化しませんか？

1040

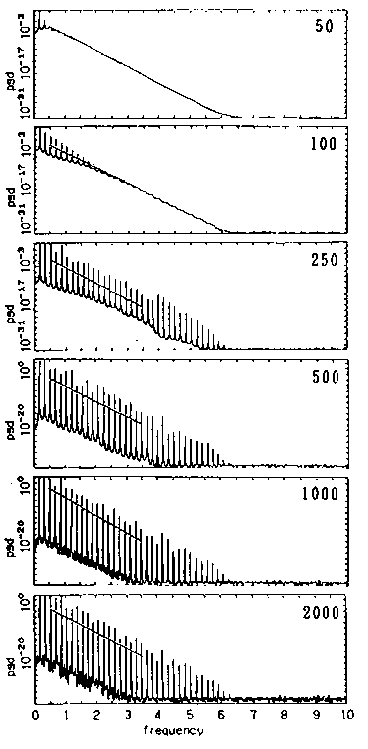
答　図1040に，c =2.55 の値におけるレスラー・モデルから計算された時系列データに対するMEM-PSDを示します(レスラー・モデルの式については，問1320を参照して下さい)．この図から，50から2000にいたる広範なラグの値に対して，PSDの指数スペクトルの傾きがほとんど変化していないことがわかります．事実，これらの時系列に対して計算された指数スペクトルの傾きは，平均値で-5.507であり，平均値との誤差は最大で 2.04％です．この結果は，指数スペクトルの傾きには，ラグの値が全くといえるほど影響を与えていないことを示しています．一方，図1040からは，ラグ値の増加にともない検出される周期に対応するピークの高さが大きくなること，すなわちピークの分離が顕著になり，さらにより高い周波数成分に相当するピークが検出されてくることがわかります．これは，MemCalcが，ラグの値の増大にともない分解能が向上するというMEM本来の特性を，厳密に数値計算上実現した解析システムであることを示してます．

図1040　レスラー・モデルから計算された時系列のMEM-PSDのラグ依存性．指数スペクトルの傾きはラグによらず一定だが，MEM-PSDにおけるスペクトルの分離はラグの増加によって著しく向上している．

問　スペクトルの傾きは，時系列の測定精度によって変化しませんか？

1050

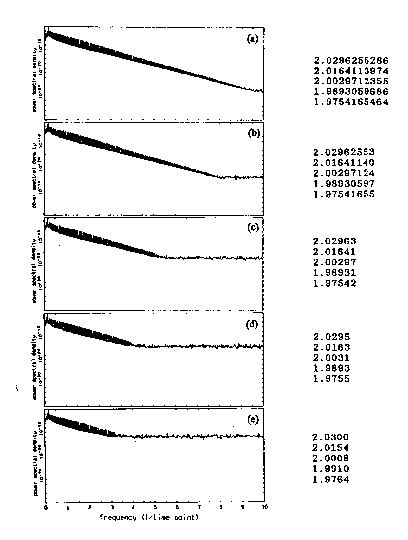
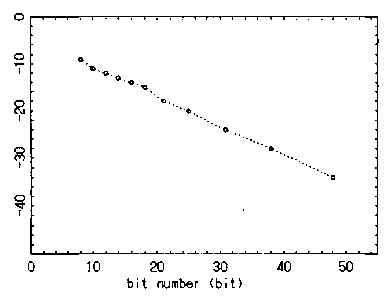
答　私たちは，カオスを含む非線形時系列に対するPSD曲線が，計算精度や測定精度の限界で平坦化するまで，周波数に対して指数的に減衰することを明らかにしました．ここで図1050_1に，c = 2.55 の値におけるレスラー・モデルから計算された時系列データについて，有効数字の桁数を小さくする操作，即ちこれは，仮想的なA/D変換器のビット数を低減しながらデータを得ることに相当すると考えられますが，こうした操作によって人為的に観測精度を落としたと見なす時系列データに対するMEM-PSDを示します．上から順に，有効桁数 11，9，6，5，5桁の時系列に対する結果であり，これらはそれぞれ38，31，21，16，12ビットのA/D変換器で観測された時系列データに対しての解析結果に相当しています．有効桁数の低減(観測精度の悪化)にともなって，PSDの平坦化するレベルが上昇してくることがわかります．図1050_2に，有効桁数(A/D変換器のビット数)とPSDの平坦化レベルとの関係を示します．PSDの平坦化レベルは，A/D変換器の分解能に逆比例し，ほぼ直線的に増加していることがわかります．表1050に，これらのPSDの傾きの値を示します．観測精度の低下により傾きを計算できる周波数領域は狭くなりますが，表1050からわかるようにPSDの傾きにはほとんど変化が見られません．すなわち，観測精度は指数スペクトルの傾きに影響を与えないことがわかります．これは，観測精度の低下がデータに含まれる極めて微少な振幅揺らぎの検出を不可能にすること，またそれは，周波数領域において高周波成分が(ホワイト)ノイズに埋め込まれることに相当することを意味していると考えられます．一方，このことは，MemCalcが，10⁻¹² あるいは 10⁻¹³ のオーダーに関係した微少な振幅の揺らぎをも，正確に，PSDの計算に反映させるほどの高い計算精度を持つことの証明でもあります．

図1050_1　レスラー・モデルから得られた時系列に対する観測精度とMEM-PSD．A/D変換器のビット数に換算して各図のデータの観測精度は約(a)38,(b)31,(c)21,(d)16,(e)12ビットに相当する．

　

図1050_2 観測精度がMEM-PSDの下限値に与える影響．観測精度の低下によりMEM-PSDの下限値はほぼ直線的に増加していいる．

　

表1050　観測精度の悪化が指数スペクトルの傾きに与える影響．観測精度の悪化にともない指数的に減衰する周波数範囲は減少するが，指数スペクトルの傾きにほとんど変化が見られない．

問　MemCalcシステムでは時系列データに対するあてはめ曲線を求めるとき，この曲線として複数の余弦函数に水準値，または傾向線を加えた函数形を使用しています．さまざまな函数形が考えられると思いますが，なぜそのようにしたのですか？

1060

答　一般に時系列データの変動の従うべき理論式は，未知です．その場合，単純，かつ汎用性の高い解析函数を時系列データにあてはめることが最も有用であると考えられます．
　MemCalcシステムではこの函数形として水準値，または傾向線に複数の余弦函数からなる合成函数を採用しています．この合成函数はさまざまな時系列データへのあてはめを想定したものとしては極めて単純ですが，同時に，あらゆる変動が余弦函数の重畳としてのフーリエ級数展開により完全に記述できることを考えると，極めて汎用性・柔軟性の高いものとなっています．更に，余弦関数を用いることにより，現実に得られる有限長データをスペクトル解析理論に要求される(−∞，＋∞)への時間領域の拡張を可能にする数学的基底を与えています(問0900参照).
　なお，フーリェ級数展開では基本周期Tと無限個のその高調波によって変動を完全に記述します．MemCalcシステムではスペクトルピークから有限個のモードを取りだしてこれらのモードの重畳として原データを再現しますが，この手続きはフーリエ級数展開で基本周期Tを充分に大きくとり，級数を構成する無限項のうちの所定のモードだけを用いて原データを再現することに対応します．MemCalcシステムにおいて水準値，または傾向線はMEMスペクトルにおいて検出し得なかった極低周波数帯のピークの示すモードに対応します．

問　MemCalcというプログラムは観測装置・実験装置であると聞きました．それはどういうことですか？

1065

答　実験屋はその時代それぞれに利用可能な資源・技術などの制約のなかにあって，工夫の限りを尽くしてさまざまな観測装置・実験装置を組み上げてきました．そしてそれら観測装置・実験装置のもたらすデータの真に意味するところを理解しようとする努力のなかで対象系に関する理解が深まり，ときとして新しい理論体系の誕生を見たことは科学史の一面の真実です．このとき，共通の物理法則・化学法則のもとにあるにも関わらず，然るべき実験屋が目的を持って真摯に組み上げた装置はそうでない装置に比較して格段の性能を発揮し，科学に大きく貢献してきました．
　電子計算機のプログラム(数値計算プログラム)は物理法則・化学法則の制約を直接に受けるわけではありませんが，しかしその時代のハードウェアの限界・ソフトウェアの性能という制約の下で工夫された一種の数値実験装置であることを忘れてはなりません．すなわち，その構成如何によってそのもたらすデータの精度が大きく異なることを忘れてはなりません．そしてこの差は実験装置が複雑であればあるほど拡大されます．MEMのプログラムが正にこの場合にあたります．
　すなわち，一般的なMEMのプログラムなどというものは存在せず，MEMという理論体系の実現としてのMemCalcという数値実験装置，またはその他の実験装置があると理解しなければなりません．
　今日，科学の進展に伴い，多くの場合に研究者自らが実験装置を組み上げることはますます困難になってきています．このとき，上記のように考えるならば(数値)実験装置に対してユーザーはどのような態度で臨むべきであるかが自ずと明らかとなります．複雑な実験装置についてはユーザーがその構成を完全に理解することは金輪際不可能であり，ユーザーはその運用結果を通してのみ，装置の妥当性を窺い知ることができます．そして多くのユーザーがこの装置を用いて行ったさまざまな結果について，それぞれ実験対象に関する専門家の立場から検討し，それが妥当であると結論づけるならば，間接的に実験装置そのものの妥当性が検証されたことになります．また，このことはすなわち，(数値)実験装置はそのような検証の手段をユーザーに提供しなければならず，それを持たない装置(例えば特定の種類のデータのみを扱い，他と比較できる量を出力しない装置)は少なくとも単独で使用されるべきではありません．今日，ユーザーにはこのような視点で実験装置を選択することが求められています．そしてMemCalcは当初からまさにそのような(数値)実験装置として構成されています(MemCalcが当初想定したユーザーはスペクトル解析の専門家です)．
　蛇足ですが，数値計算プログラムを数値実験装置として捉えるとき，例えば｢FFTでも計算して検証したか.｣などという質問がどれほど的外れなものであるかが明白となります．この質問は通常，研究者にFFTのプログラムを組んだ上でその結果を検討することを求めています．しかしながら数値計算の専門家ならばいざ知らず，その余のユーザーがFFTとはいえ簡単に実用レベルの数値計算プログラムが組めると考えること自体，数値計算の怖さを知らない素人のあさはかな発想です．また，仮に既存のFFTのプログラムを使用することを求めているのだとしても，FFTはその適用の段階でさまざまな選択肢があり，使いこなすのは容易なことではありません．従ってこの場合に発すべき質問は｢FFTでも計算して検証したか.｣ではなく｢従来FFTを用いて同様の研究がなされてきているが，得られた結果はそれらと比較してどうか．またそれはなぜか.｣ということになります．

↑ページの先頭へ

←　その１(/２）へ