←　前節(§§４−３)へ
↑百問百答目次へ
→　次節(§§５−１)へ

§４　実データのMemCalcによる解析
§§４−４　論文閲読者の指摘と著者の回答

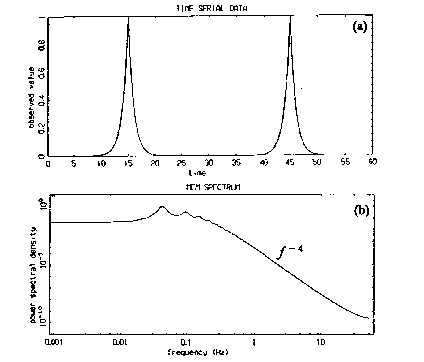
私達は，カオス時系列に関するMemCalcによる解析結果を一連の論文に公表してきましたが，本節ではそれらの論文に対する論文閲読者と著者らの回答を紹介します．　

問　(参考文献2-3に対する閲読者の意見) レスラーモデルで，a =0.2，b=0.2，c=2.6のとき，レスラー方程式は周期解をもち，その周期解はアトラクターである．初期条件X0=Y0=Z0=1.0から始まる軌道はこの周期解に漸近する．ここまでは論文の著者に従う．以上のことから，この軌道についてのパワースペクトルS(f)は離散的であることが結論できる．著者のパワースペクトルの推定値にはexp(-λf)なる成分がほぼ連続的に現れる．これは本来のパワースペクトルS(f)には含まれ得ないものである．従って，推定という操作に伴って付加されたアーティフィシャルなものと考えれる．a=0.2，b=0.2，c≧4.3ではパワースペクトルS(f)は連続成分を持ち得る(カオスの場合)．著者による推定値に現れるexp(-λf)なる成分は，上のc=2.6の場合の連続成分とほぼ対応した形状を持つ．従って，この場合も同じ原因によるアーティフィシャルである可能性が大きい．本来のパワースペクトルS(f)の連続成分にexp(-λf)なる成分が含まれているとする根拠は不十分である．

1870

答　一般に，周期性をもつ時系列のスペクトルは，基本波とその高調波に対応した一群の線スペクトルからなるとともに，高調波領域における線スペクトルは，強度の変化傾向をもつことは勿論であり，その時系列の波形(一周期内の連続した変化，あるいはある連続した振幅変調は周波数変調など)に対応した強度変化形状をもちます．
　これまでのカオス研究では，このパワースペクトルが巾乗で減衰，例えば，1/f や1/f 2であるのか，指数減衰であるのか，議論されてきました．我々の前報と今回の結果は，これが指数減衰であることを，直接的なスペクトル計算によって，明瞭に示した重要なものであると考えております．
　レスラー．モデルやローレンツ・モデルなどの時系列のパワースペクトルの高調波数領域における特性が，未だ理論的に明らかになっていない段階では，実験的研究が重要であることは言うまでもないことです．我々の前報や今回の論文は，数値実験としての意味を持ちます．
　数値実験によって得られる結果は，そこにアーチフィシャルな影響がどの程度入っているかの検討は勿論のこと，その結果についての慎重な吟味が必要となります．その場合，計算精度について我々がなし得ることは，理論的に導出可能な時系列のスペクトルについてテストすることです．
　それ故，我々が用いた(MEMのBurg法に基づく)計算アルゴリズムによるスペクトル推定の精度については，その一部を前報で具体例を挙げて示した通りです．従って，今回の論文原稿には改めてこれについての記述をしませんでした．
　参考のために，計算アルゴリズムの精度のテストの具体例として，スペクトルが解析的に求められる場合の計算結果を一，二添付します．
　一つは，指数型波形

　　x (t) = exp(- C | t | ), C > 0,  -T0 / 2≦  t ≦ T0 / 2

を１周期とする周期時系列で，C = 1，T0 = 30の場合について，図1870-1(a)に示してあります．このパワースペクトルP (f )は解析的に求められ，{1 / (1 + f 2)}に比例し，f ≫1の領域で f -4減衰，つまり，

　　ln P ( f )  〜 -  4 ln f

となります．一方，我々が行っている数値計算による結果(図1870-1(b)は，

　　ln P ( f  )  〜  - 3 .9499 ln f

となり，理論値-4との差は1.3％程度であり全く問題になりません．
　次の例は，ガウス型波形

　　x ( t )  =  exp (- t 2)

であり，これは図1870-2(a)に示してあります．このフーリエ変換は理論的に求められ，ガウス型ですから，パワースペクトルはexp(- f 2 / 2)の形になり(図1870-2(b))，その対数をとったものは f の２次関数

　　lnP ( f )  〜 - α f 2 ＋ β

となります．一方，我々が行っている数値計算による結果は，図1870-2(c)の点線に示すものとなり，これと理論曲線(図1870-2(c)の実線)とは，高周波数領域で完全に重なります．
　以上の結果と前報の余弦波およびローレンツ型波形の時系列の結果と合わせ，我々の数値計算の精度は極めて高いものであり，時系列の高周波減衰の形状を正確に示していることがわかります．

図1870-1　指数型時系列とそのMEM-PSD．
(a)指数型時系列，(b)両対数表示によるMEM-PSD．

　

図1870-2　ガウス型時系列とそのMEM-PSD．
(a)ガウス型時系列，(b)MEM-PSDの両対数表示，(c)MEM-PSDの片対数表示．

問　(参考文献2-3に対する閲読者の意見) レスラー系のカオス状態はバンドカオスを構成しています．この場合，系のパワースペクトルは周期成分と連続成分との直積になります．周期成分はバンドアトラクターを周回する基本周期とその高調波です．連続成分はカオスの混合性に由来するものです．なお，ローレンツ系の通常のパラメータ領域ではバンド構造はなく，そのパワースペクトルは連続成分のみです．
　さて，｢レスラー系のパワースペクトルが指数型である｣との主張は次のどちらでしょうか．

‡@周期成分の高調波が指数型である．
‡A連続成分が指数型である．

レスラー系のカオス状態に対して，論文では，周期成分と連続成分の合成されたパワースペクトルしか計算していません．バンドカオスから分岐によって周期状態の｢窓｣が生じます．論文の計算では，カオス状態と｢窓｣とでパワースペクトルの計算結果がよく似ています．とくにその指数の値がよく一致しています．窓の状態での周期は分岐によって生じるバンドカオス状態の周期成分と連続的につながることが知られています．
　以上のことから，論文の内容は‡@の主張しかできないと思います．しかし，乱流の間欠性とからんで問題になっているのは‡Aの内容ではないでしょうか．

1880

答　私達が，本論文において明らかにした主要な点は次のことにあります．

１． レスラー方程式から数値計算によって得られる時系列解析のパワースペクトル密度(PSD)は，計算精度の限界まで指数特性を示す．この指数特性は，データ長の有限性が現れている低周波数領域を除き，方程式のパラメータ値やデータ長に関わりなく観測される．
２． PSDに観測される一連のピークは，周期倍分岐過程および逆カスケード過程の振舞いを正しく示し，この両過程の境界に特異な振舞いが観測される．
３． 基本周期モードのパワーは圧倒的な強度をもっている．

　これらの諸点は，これまでのカオス研究では十分明らかになっているとは言い難い内容を含むものです．とりわけ，カオス時系列のPSDの指数特性については論文中で記述したように，多くの実験的・理論的研究が報告されているにも関わらず，1/f 特性ほど注目されていたわけではありません．私達が行った指数特性の系統的確認は，計算精度の厳しい検討を踏まえた数値計算によって初めて可能になったものであり，PSDそのものが指数特性を示すという事実を明らかにした本論文は，重要な意義をもつものであることが判断されます．
　閲読者は，この指数特性が，周期成分の高周波特性であるのか，連続成分の特性であるのか，いずれかを明確にするように求めておりますが，私達は，以下の理由によって，この閲読者の求めに応じることはできません．

１． 時系列が連続成分と周期成分を併せ持つ場合，一般的に，与えられた時系列の周期成分と連続成分の分離可能性は保証されません．特に，レスラー系のような非線形な系では，なんらかの理論モデルや仮定の導入なしには，周期成分と連続成分を分離できるものではありません．
２． 非線形微分方程式系の数値計算によって得られた時系列は実験によって得られた時系列から，それらのPSDを求める場合，当然無限長の時系列ではなく，有限長の時系列を対象にすることになります．この場合，有限長という制限は，PSDの連続成分と周期的成分の両者に影響を与えます．この意味からも，連続成分を分離することは不可能です．
３． 前報で示したように，レスラー系やローレンツ系のより長いデータ長の時系列のPSDでは，高周波数領域において離散的ピークが殆ど見られず，連続成分が支配的であるように見えます．従って，この高周波数領域では，PSDの連続成分は指数特性を示すと言ってよいかもしれません．しかし，これが連続成分であると決定する根拠は今のところありません．

　本論文は，全PSDそのものが，非線形微分方程式系のパラメータ値に関わらず，指数減衰を持つことを明らかにしました．その上で，指数特性が周期成分の高調波の特性であるのか，連続成分の特性であるのか，あるいはその両者に共通した特性であるのか，などの解明は，今後の重要な理論的研究課題であると考えます．

問　(参考文献2-3に対する閲読者の意見) さて，｢レスラー系のパワースペクトルが指数型である｣との著者の主張は次のどちらでしょうか．　　

１． 周期成分の高調波が指数型である．
２． 連続成分が指数型である．

なぜ，このように申し上げるのか，その背景について述べます．

１． ｢スペクトルの周期成分が指数減衰を示す｣との主張はトリビアルです．なぜなら，周期関数のフーリエ成分について，その高調波の速やかな消失がその周期関数の十分ななめらかさを意味することはすでに知られていることです．レスラー系のようななめらかな常微分方程式の解として得られる周期解が十分なめらかなものであったことを確認したに過ぎません．
２． ｢スペクトルの周期成分が周期倍加分岐過程および逆カスケード過程の振舞いを反映する｣ことは，すでに知られていることです．このスペクトル推定法の精度の確認をすることにはなっても，本論文の新たな発見とは言えません．

　以上のことから，本論文が意味のあるものとなるのは，本論文の結果がスペクトルの連続成分に関して何事かを示唆するものである場合に限られると思います．スペクトルの周期成分と連続成分の分離が完全にできないという理由によって，連続成分に関する主張を明確にしないままでは論文としての価値が低いというのが閲読者の判断です．
　著者がこの論文に示された計算結果の範囲で，スペクトルの連続成分に関してどのように推測しているかを論文に明記するべきです．この点が明確になれば論文としての価値があるし，その推測の真偽は，公の場で今後の議論によって明らかになっていくものと考えます．

1890

答　PSDの連続成分に関する考察を記述するため，§6 Discussion and Concluding Remarks の最初に，6.1 Fluctuations and route to chaos という新たな項目を挿入しました．
　閲読者の｢『スペクトルの周期成分が指数減衰を示す』との主張はトリビアル｣というご意見には賛成できません．ご指摘の通り，｢高調波の速やかな消失がその周期関数の十分な滑らかさを意味する｣ことはもちろんです．しかし，高調波が指数減衰しなければならない(しかも，かなり低い次数から指数減衰しなければならない)という時系列の性質はトリビアルなことではないと考えます．この点については，§6の6.3に若干の加筆をしました． 

問　(参考文献2-3に対する閲読者の意見) c=2.6での f1/2にあらわれる連続成分を連続スペクトラムの起源とする考えですが，かならずしも承伏しかねます．この部分は，ローレンツ型スペクトルで，レスラー方程式にホワイトノイズを加えたときに生じ，この外部ノイズを小さくするにつれて消失していく性質をもっています(閲読者の経験)．常微分方程式を数値的に積分すると，数値の丸め誤差のためにこの種の外部ノイズを加えたのと同じ減少を観測することだと解釈しています．スペクトルの統計的推定という操作と，この点がどう絡んでくるかという問題は議論の余地が残ります．ともあれ，この種の決定論的なシステムに現れるスペクトルの連続成分については，まだまだ明確に理解されていない面が多いと思います．証明があるのは，｢その系のポアンカレ写像がルベークスペクトルを持つならば，スペクトルは連続成分を持つ｣ということです．このような抽象的な条件が実際にどうなっているのか，具体的に調べていく必要があると思います．

1900

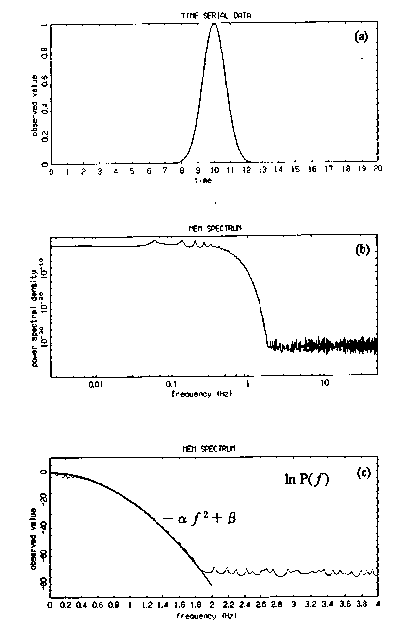
答　閲読者のご意見は，c = 2.6の f 1/2の位置に現れている連続スペクトルは，常微分方程式を数値積分するときの丸め誤差に起因していると解釈される，ということにあると思われます．丸め誤差の問題は厳しいチェックが必要なところです．そのため，前回の再提出本論文にいおいて，スペクトル計算の他に時系列そのもので確認するために，10-33の精度で計算した時系列の振幅を詳細に調べ(この時系列にちおいては本論文§6.6で考察されています)，f 1/2モード位置の成分を発生させる振幅ゆらぎを直接観測してFig.8で示し，その変動が10-4であることを明示しました．更に言えば，これが丸め誤差および本論文で用いた数値計算アルゴリズムに起因する誤差の結果でないことは，10-19の精度の計算による時系列のbifurcationおよびinverse cascadeの各過程で，f 1/4，f 1/8等の低レベルの線スペクトルが正確に得られていることからも裏づけられます．

問　(参考文献2-2に対する閲読者の意見) カオスのどのような特徴が指数PSDに反映されるのですか？

1910

答　本論文の最も重要な点は，ローレンツカオス系などの非線形時系列のPSDが指数型スペクトルをもっていることを示したところにあります．この指数型スペクトルとカオスとの関係については，今後の詳しい研究が必要であり，その点は§5.6 Concluding Remarksの末尾に述べました．

↑ページの先頭へ

←　前節(§§４−３)へ
↑百問百答目次へ
→　次節(§§５−１)へ